For some important aspects of Internet engineering, most notably IP Addressing, an understanding of binary arithmetic is critical. Many strange-looking decimal numbers can only be understood by converting them (at least mentally) to binary.
All digital computers represent data as a collection of bits. A bit is the smallest possible unit of information. It can be in one of two states - off or on, 0 or 1. The meaning of the bit, which can represent almost anything, is unimportant at this point. The thing to remember is that all computer data - a text file on disk, a program in memory, a packet on a network - is ultimately a collection of bits.
If one bit has two different states, how many states do two bits have? The answer is four. Likewise, three bits have eight states. For example, if a computer display had eight colors available, and you wished to select one of these to draw a diagram in, three bits would be sufficient to represent this information. Each of the eight colors would be assigned to one of the three-bit combinations. Then, you could pick one of the colors by picking the right three-bit combination.
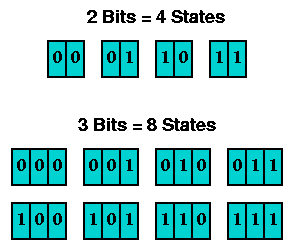
A common and convenient grouping of bits is the byte or octet, composed of eight bits. If two bits have four combinations, and three bits have eight combinations, how many combinations do eight bits have? If you don't want to write out all the possible byte patterns, just multiply eight twos together - one two for each bit. Two times two is four, so the number of combinations of two bits is four. Two times two times two is eight, so the number of combinations of three bits is eight. Do this eight times - or just compute two to the eighth power - and you discover that a byte has 256 possible states.

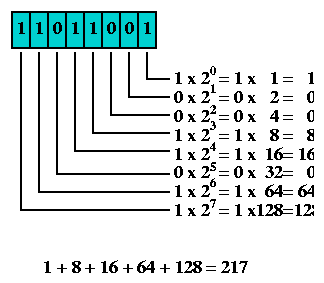
Obviously, if a byte has 256 possible states, its exact state can be represented by a number from 1 to 256. However, since zero is a very important number, a byte is more typically represented by a number from 0 to 255. This is very common, and with bit pattern 00000000 representing zero, and bit pattern 11111111 representing 255. The numbers matching these two patterns, and everything in between, can be computed by assigning a weight to each bit, multiplying each bit's value (0 or 1) by its weight, and then adding the totals. For example, here's how 217 is represented as 11011001 in binary:
To convert a number from decimal to binary, begin at leftmost bit position (128). If the number is larger than or equal to the bit's weight, write a 1 in the bit position, subtract the bit's weight from the number, and continue with the difference. If the number is less than the bit's weight, write a 0 in the bit position and continue without any subtraction. Here's an illustration of converting 141 to binary:

There is a simpler way to convert bytes back and forth between binary and decimal; akin to memorizing multiplication tables. The byte can split into two four-bit halves, each half called a nibble. Memorize the decimal values for the high nibble (they're just the multiples of 16). The low nibble is trivial. Every number between 0 and 255 is the sum of one of the high nibble values and one of the low nibble values. Write the high nibble next to the low nibble, and you have the byte value in binary. Conversely, an eight-bit binary byte can be split in half, each nibble converted to decimal and two decimal numbers added together.

The most common bit patterns in Internet engineering are those with a string of one bits, followed by a string of zero bits. Here are all such bytes, along with their decimal representation, computed just like the example using 217.
